Building blocks

Representing distributions

A generative model uses:

• Prior distribution of parameters $\theta$
• conditional distribution of observations $y | \theta$

Representing distributions

A generative model defines:

• Prior predictive distribution of $y$: $$p(y)= \int p(y, \theta) d\theta$$
• Posterior distribution of $\theta$: $$p(\theta|y) = \frac {p(\theta)p(y|\theta)} {\int p(\theta)p(y|\theta)d\theta} \propto p(\theta)p(y|\theta)$$
• Posterior predictive distribution of $\tilde y$: $$p(\tilde y | y) = \int p(\tilde y|y, \theta)p(\theta|y)d\theta = \int p(\tilde y|\theta)p(\theta|y)d\theta$$

Approximation by samples

• In some models, distributions are available in closed form. Example — Beta-Bernoulli:
• In most models, no closed form. We approximate distributions by samples.
• How can we summarize the posterior in a few numbers. And why should we?

Summarizing samples

• Summary statistics
• Point estimates
• Compatibility intervals

Summary statistics

• Mean, standard deviation(, skew, kurtosis, ...)
• Fully defines known distributions
• Gives information about shape
• Can be misleading: Beta, Normal, Gamma

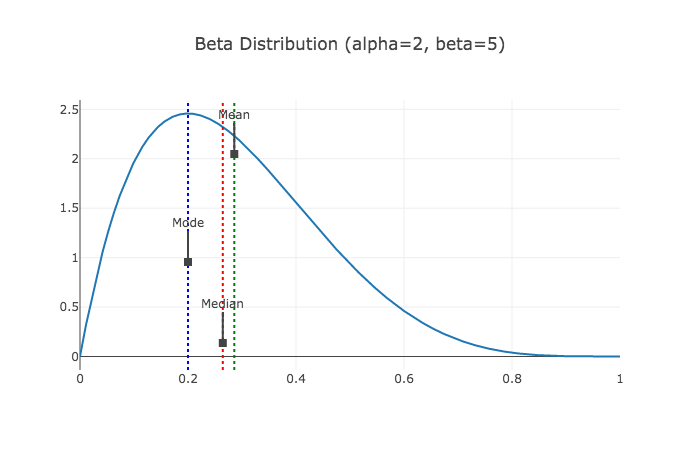
Point estimates

• Mean: $\mathrm{mean} = \mathbb{E}(x) = \int x p(x) dx$
• Median: $\Pr(x \le \mathrm{median}) = \Pr(x \ge \mathrm{median})$
• Mode: $\mathrm{mode} = \arg \max p(x)$

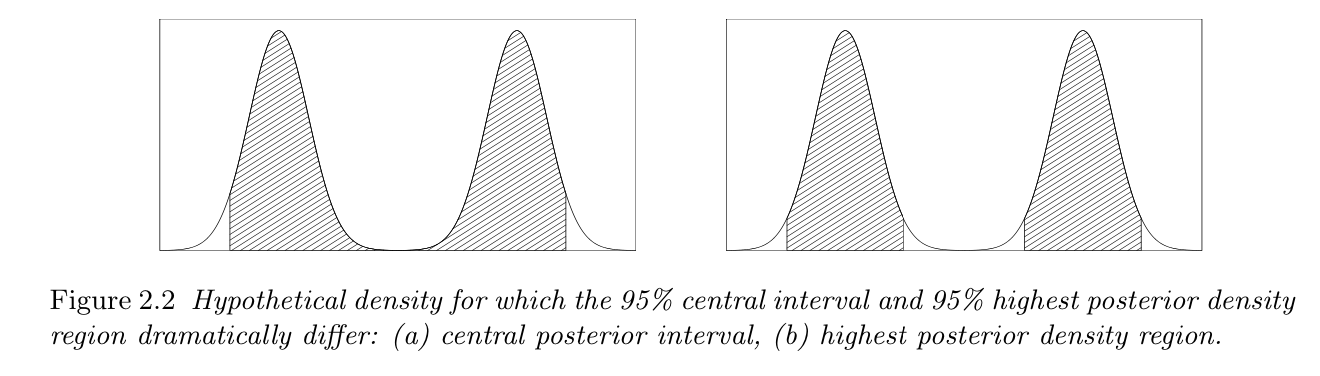
Compatibility intervals

• Central intervals — ‘quantiles’
• Highest posterior density regions

Some ‘standard’ models

Normal distribution

Sum of many random variables: Galton board

Example: human height and weight

Height and weight Kaggle dataset

Poisson model

• Conditional probability: $$p(y|\theta)=\frac {\theta^y e^{-\theta}} {y!},\mbox{ for }y=0,1,2,...$$
• Rate and exposure $$y_i \sim \mathrm{Poisson}(x_i\theta)$$
  • $x_i$ — exposure, known
  • $\theta$ — rate, unknown

Example: cancer rates

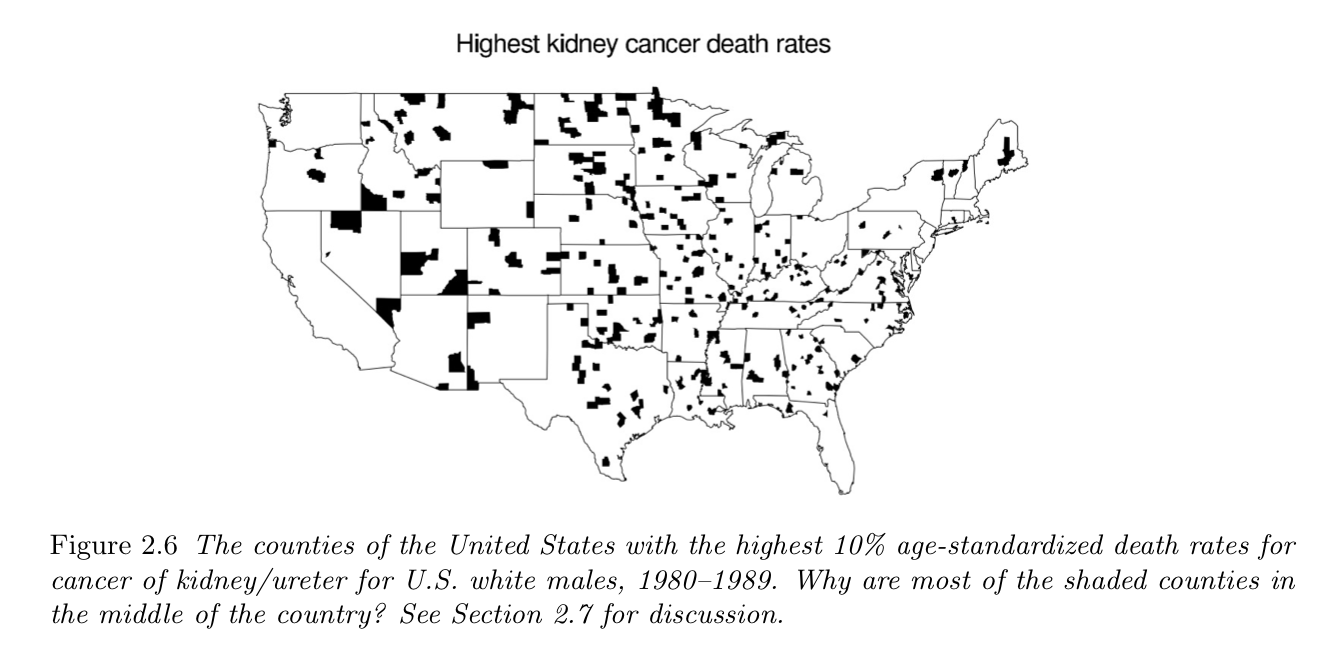
Example: cancer rates

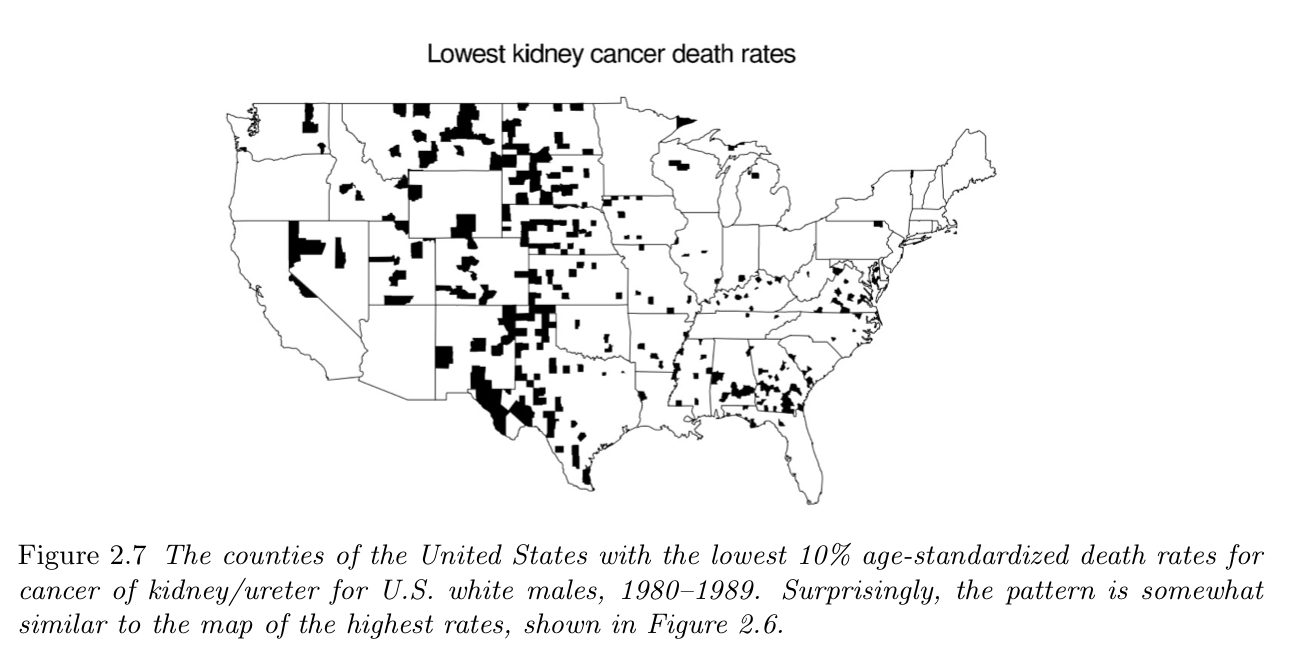
Example: cancer rates

Model

• Sampling distribution: $y_i \sim \mathrm{Poisson}(10n_j\theta_j)$
• Prior distribution: $\theta_j \sim \mathrm{Gamma}(20, 430\,000)$
• Posterior disribution: $\theta_j|y_j \sim \mathrm{Gamma}(20+y_j, 430\,000 + 10n_j)$

• Small county: mostly prior
• Large county: mostly observations