Model checking

Model checking in Bayesian data analysis

• Is the model adequate?
• Where is the problem?
  • prior
  • sampling
  • hierarchical structure

Sensitivity analysis and model improvement

• How does the posterior change
• A model may be adequate but sensitive
Is our model true or false?
Is the model good enough for our use?

Does the inference result make sense?

• Is important knowledge omitted from the model?
• External validation
• Choice of predictive quantities

External validation

• New data to check the model.
• Example: Michael Levitt and Corona

Choosing predictive quantities

• Analysis depends on what we predict.
• In hierarchical model we can predict (school, rats):
  • Either new group
  • Or new items in existing groups

Posterior predictive checking

Our models are generative

• Draw samples from predictive posterior.
• Compare the draws to the data.

Example: Newcomb's speed of light

Notation for replications

• Replicated data: $y^{\mathrm{rep}}$
• Same explanatory variables $x$ as in $y$
• Posterior predictive of $y^{\mathrm{rep}}$: $$p(y^{\mathrm{rep}}|y)=\int p(y^{\mathrm{rep}}|\theta)p(\theta|y)d\theta$$

Test quantities

• discrepancy measures — aspects of the data we want to check
• $T(y, \theta)$ or $T(y^{\mathrm{rep}}, \theta)$
• Posterior predictive p-values — $$p_{B}=\Pr(T(y^{\mathrm{rep}}, \theta) \ge T(y, \theta)|y)$$
• In practice, use simulation to compute $y^{\mathrm{rep}}$ and $p_{B}$

Test quantities

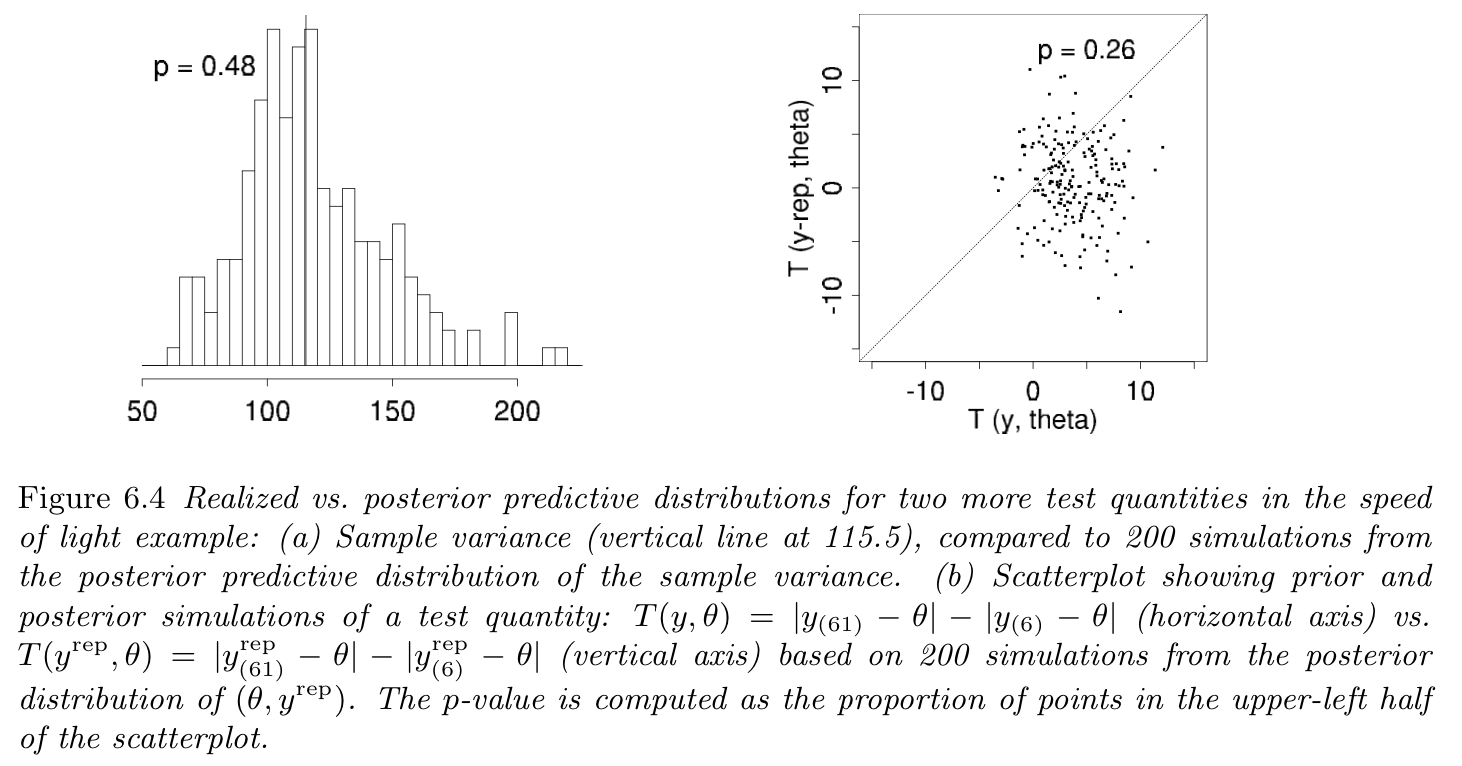
Choosing test quantities

• Should depend on data `more' than on parameters
• Can use several test quantities for different aspects

Example: globe tosses

Interpreting p-values

• Quantifying discrepancies between data and model
• Limitations of posterior tests:
  • Adequate model can be bad ($\tau = 0$)
  • `Bad' model can work in some cases

Marginal predictive checks

• Compute for each $y_i$: $$p_i = \Pr(T(y_i^{\mathrm{rep}}) \le T(y_i)|y)$$
• Sometimes, best $T(y)$ is $T(y) = y$: $$p_i = \Pr(y_i^{\mathrm{rep}} \le y_i|y)$$
• Example — 8 schools:
  • Marginal for each existing school
  • Margin for a new school
• Cross validation: $$p_i = \Pr(y_i^{\mathrm{rep}} \le y_i|y_{-i})$$

Graphical posterior predictive checks

• Direct data display
• Summary statistics
• Residuals

Direct data display

Summary statistics

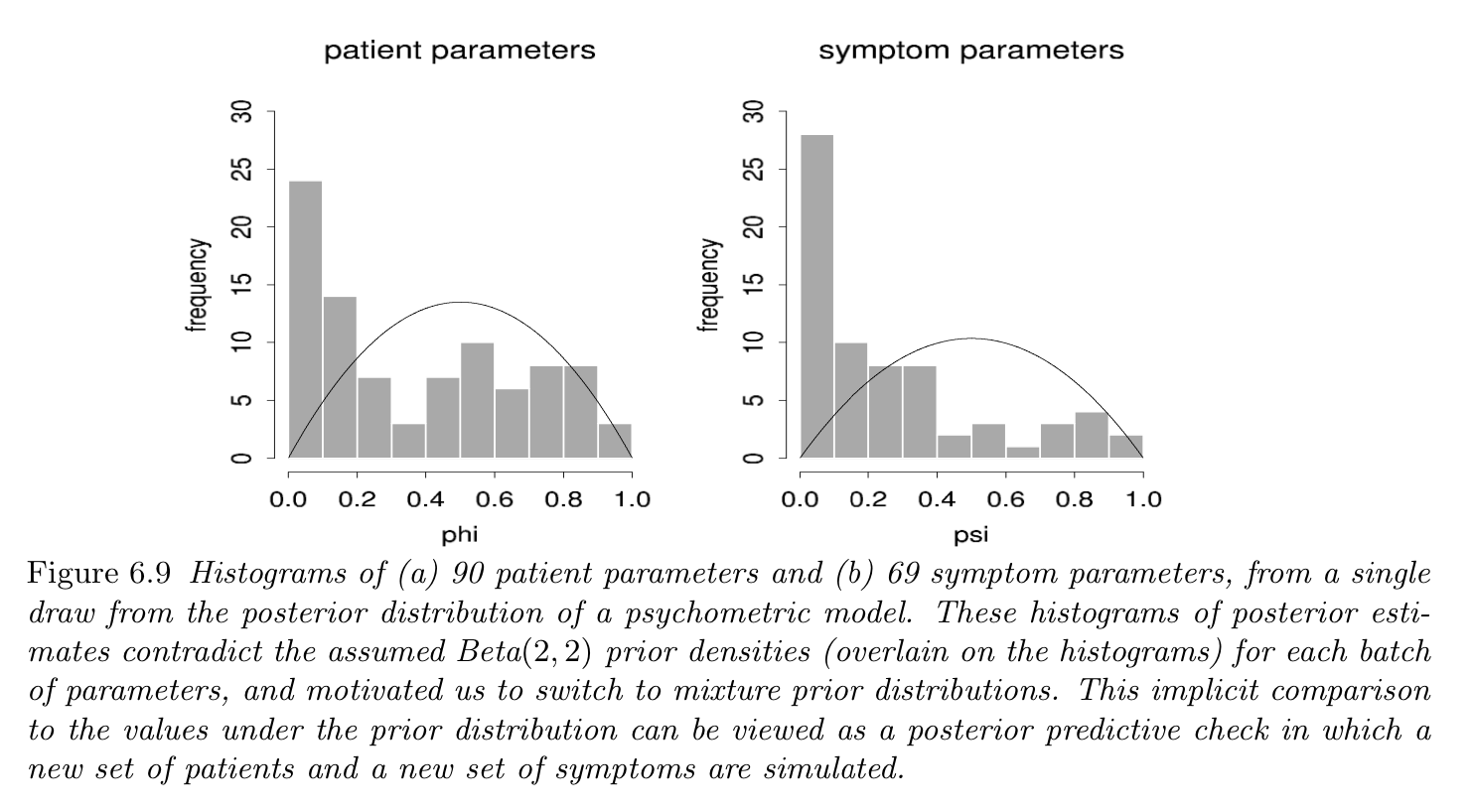
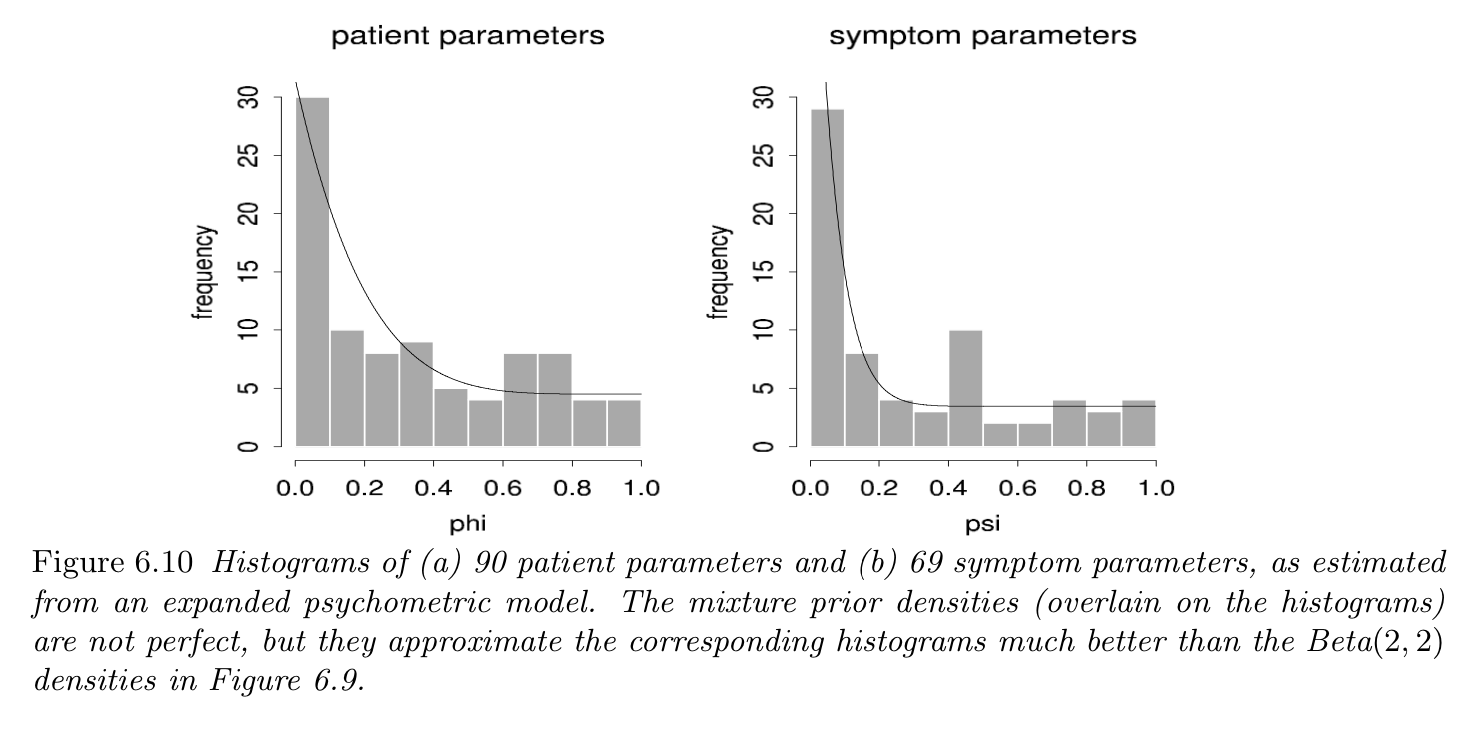
Summary statistics

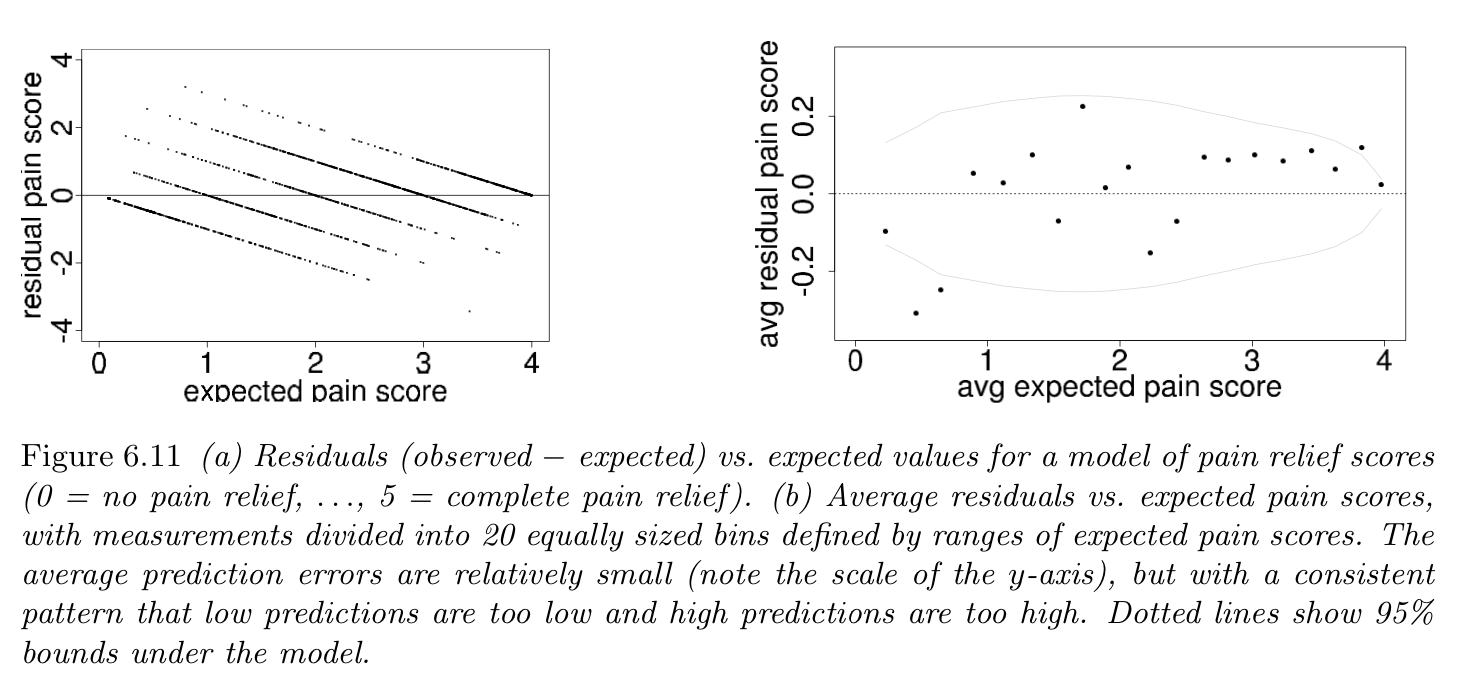
Residuals

Model checking on 8 schools

Assumptions:

1. $y_j \sim \mathcal{N}(\theta_j, \sigma_j)$
2. $\theta_j$ exchangeable
3. (?) $\theta_j \sim \mathcal{N}(\mu, \tau)$
4. (?) $p(\mu, \tau) = C$

Posterior predictive checking

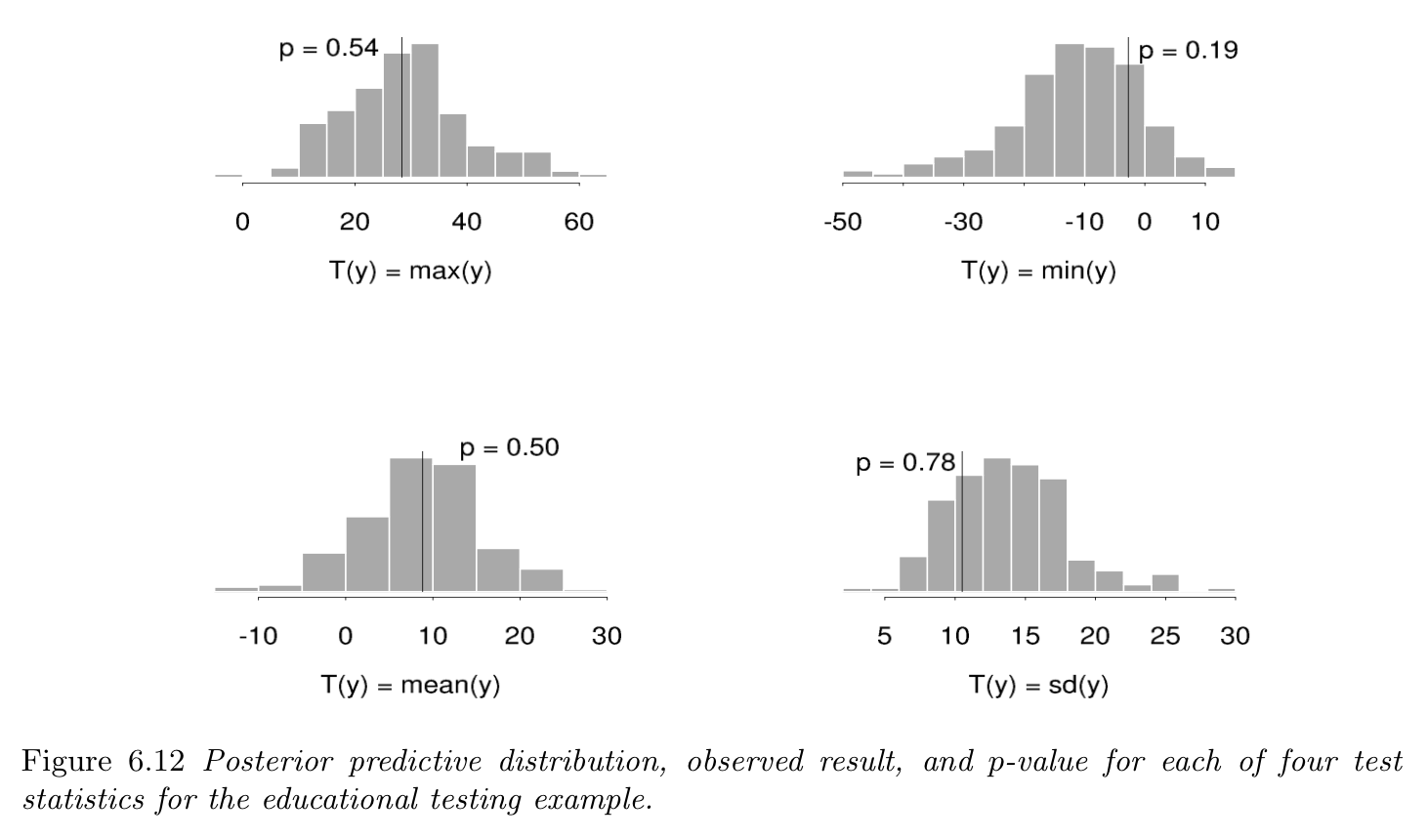
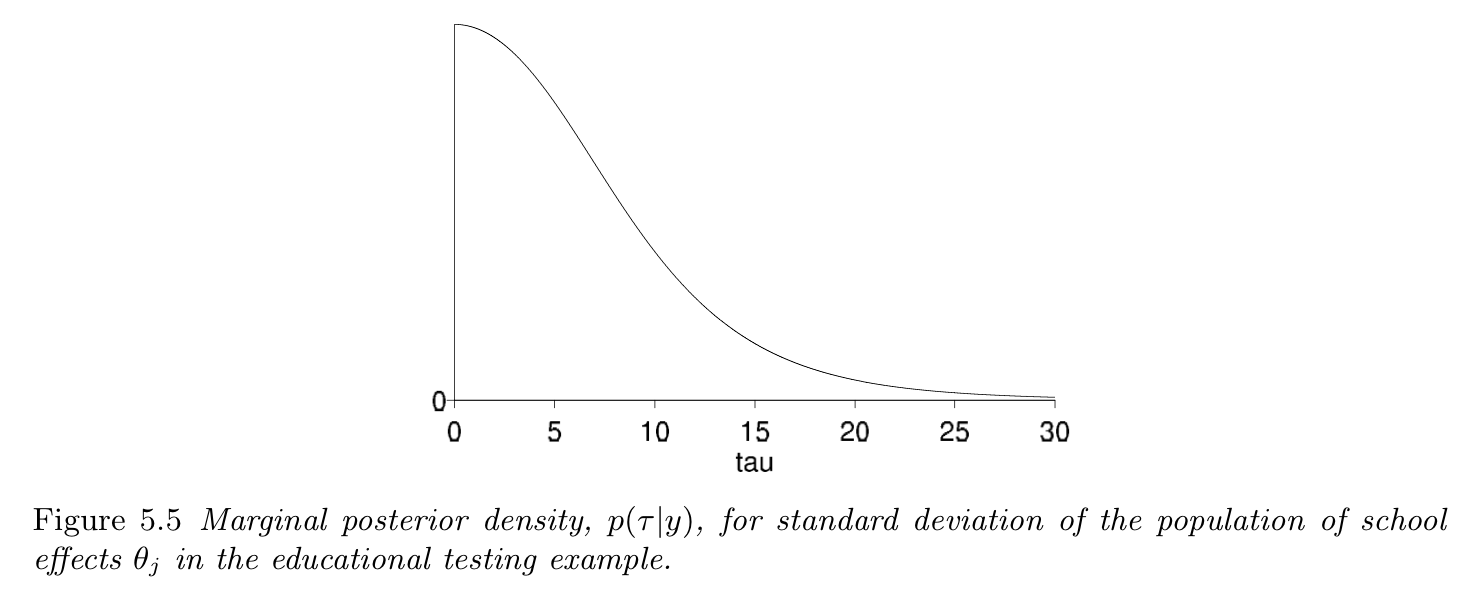
Sensitivity analysis