Finite mixture models

Setting up mixture models

• Population consists of subpopulations
• Like hierarchical models, only we groups are not given
• Random indicators are used to specify subpopulation (unknown) of each observation
• Subpopulations == components

Finite mixtures

• We model distribution of $y=(y_1, ..., y_n)$ as a mixture of $H$ components
• Component distribution $f_h(y_i|\theta_h)$ depends on parameters $\theta_h$
• Proportion of population from $h$th component is $\lambda_h$, $\sum_{h=1}^H\lambda_h=1$

Sampling distribution

The sampling distribution: $$p(y_i|\theta, \lambda) = \lambda_1 f(y_i|\theta_1) + ...+ \lambda_H f(y_i|\theta_H)$$

LogSumExp: $$\log p(y_i|\theta, \lambda) = \log (\lambda_1 \exp (\log f(y_i|\theta_1)) + ... $$ $$+ \lambda_H \exp(\log f(y_i|\theta_H)))$$

Sampling from sampling distribution

For each $i$:

1. $z_i \sim Categorical(\lambda)$
2. $y_{i} \sim F(\theta_{z_i})$

Identifiability of the mixture model

• Parameters are not identified if different parameters result in the same likelihood
• Mixture models are unidentifiable because labels can be switched (GMM in Stan example)
• How to fix:
  • specify order of mixture components or mixture weights
  • hierarchical mixture models

Number of mixture components

How many componentst?

1. Guess (2 components for heights of humans)
2. Try different values and compare (Chapter 7)
3. Infer - $H \sim D$; what should be D

Philosophy: meaning of mixture models

1. One opinion: mixture models learn latent true structure
2. Another opinion: mixture models approximate multi-modal distributions
3. Both

Example: reaction time in schizophrenia

Dataset http://www.stat.columbia.edu/~gelman/book/data/schiz.asc

• Response times measured for 11 non-schizophrenics and 6 schizophrenics
• Schizophrenics are
  • slower to respond
  • sometimes lack attention
• ⇒ Hierarchical model with mixture for schizophrenics

Reaction time: Data

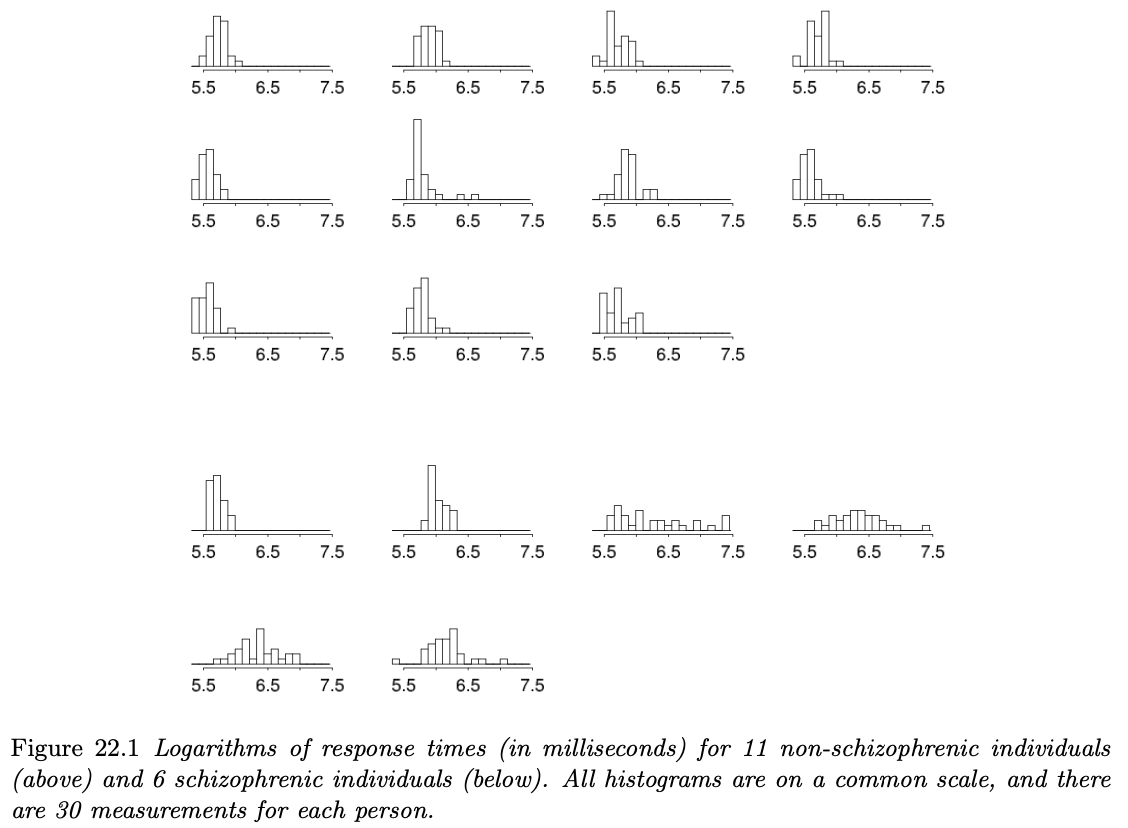
Reaction time: Parameters

• $x_j$ — schizophrenic, $y_{ij}$ — response time
• $\lambda$ — probability of delay
• $\tau$ — delay
• $\alpha$ — response time without delay
• $\mu$ — average response time
• $\beta$ — slow down in schizophrenics

Reaction time: model

for j in patients: $\alpha \sim \mathcal{N}(\mu, \sigma^2_\alpha)$ if $x_j$: # schizophrenic for i in trials: $z \sim \mathrm{Bernoulli}(\lambda)$ if $z$: # lack of attention $y_{ij} \sim \mathcal{N}(\alpha + \beta + \tau, \sigma^2_y)$ else: $y_{ij} \sim \mathcal{N}(\alpha + \beta, \sigma^2_y)$ else: for i in trials: $y_{ij} \sim \mathcal{N}(\alpha, \sigma^2_y)$